线性代数在考研数学中占有重要地位,须予以度重视。线性代数试题的特点比较突出,以计算题为主,证明题为辅,因此,须注重计算能力。线性代数在数学二中占20%左右。2021年考研数学中线性代数共五道题目,(3道选择题+1道填空题)*5分+1道解答题12分=32分。
下面剖析一个经常出现的考试要点——二次型。首先,要求掌握二次型及其矩阵表示,让我们看一下2013年数学一二三考研试题:

由于二次型与它的实对称矩阵式一一对应的,所以二次型的很多问题都可以转化为它的实对称矩阵的问题,可见正确写出二次型的矩阵式处理二次型问题的一个基础。我们分析

其次,我们需要了解了解二次型的秩和标准形等概念,其中二次型的秩可以通过矩阵的秩加以研究,而标准形要注意区分是正交变换法下的标准形还仅仅是非退化的线性变换,前者保持特征值不变,后者仅仅能够保持正负惯性指数不变(特征值的符号/正负特征值的个数)这一点我们接着看这道试题的第二小问:

再次,需要特别注意的是我们还需要了解二次型的规范形和惯性定理(2018年大题、2019及2021年选择均有涉及);掌握用正交变换并会用配方法化二次型为标准形(这点在2020年数学二大题有所考察);这里需要单独把2020年试题单独拎出来给大家说明:
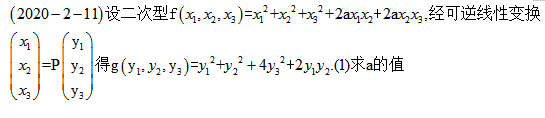
而数学二的试题仅仅是可逆的线性变换,所以仅仅能说明对应矩阵是合同的,即转化为对应的秩相同,可以解得
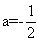
二次型最后一个需要注意的考试要点是需要同学们理解正定二次型和正定矩阵的概念及其判别方法。重点题型有:二次型正定性的判别和证明。这部分历年试题共出现过十道题目,总结题型如下,一数值型利用顺序主子式求参数,二是抽象型利用特征值判定,三是证明题一般利用的是定义(需要注意不要忘记所需证明的二次型矩阵一定要先证明是实对称矩阵)。以上就是关于线性代数中关于二次型的考试要点总结,希望对同学们有所帮助。






