第四节 数据分析
一、基础统计分析
(一)描述统计分析
1.集中趋势的测度
集中趋势是指一组数据向其中心值靠拢的倾向,测度集中趋势就是确定数据一般水平的代表值或中心值。集中趋势的测量有三个常用的指标:
(1)众数,是一组数据中出现次数最多的变量值。
对数据确定众数时,只需把数据整理后列出频数(出现次数)分布表,频数最多的那一组为众数。从分布图形来看,众数应对应于图形最高点。有些情况下数据分布可能表现为双众数,甚至多众数,也有另一种情况,即没有众数(均匀分布)。众数的基本思想,是用来反映一组数据若存在聚中趋势,则在数据的中心,变量值出现的频数较高,众数就是这一位置的代表值。
众数的一个突出特点是它不受极端数值的影响。
(2)中位数,是一组数据排序后处于中间位置的变量值,是一组数据的中点,即高于和低于它的数据各占一半。
(3)均值,是集中趋势的主要测度值,用于反映一组数值型数据的一般水平。主要包括算术平均数、调和平均数和几何平均数。
例子:十名学生的成绩
| 100 |
80 |
95 |
87 |
99 |
79 |
80 |
95 |
92 |
95 |
众数:95(出现3次) 中位数:
79 |
80 |
80 |
87 |
92 |
95 |
95 |
95 |
99 |
100 |
(92+95)÷2=93.5(如果数据是奇数个,则中位数就是中间那个数据)
平均数:
(79+80+80+87+92+95+95+95+99+100)/10=90.2
2.离散程度的测度
数据的离散程度是数据分布的另一重要特征,它是指各变量值远离其中心值的程度,所以也叫离中趋势。
离中趋势是经过综合与抽象后对数据一般水平的概括性描述,它对数据的代表性取决于数据的离散程度,离散程度小代表性就好,反之代表性就差。
(1)极差,也称全距,是一组数据中最大值与最小值之差。
极差是描述数据离散程度的最简单的方法,表明数据的分布范围。它计算简单,易于理解。但是极差由两端数值所决定,不能反映中间数据的分布离散状况。
(2)平均差,也叫平均离差,是各变量值(Xi)与其均值( )离差绝对值的平均数:
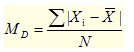
平均差反映了所有数据与均值的平均距离。平均差越小,说明数据离散程度越小。
(3)方差和标准差。方差是一组数据中各变量值与均值离差平方的平均数。方差的平方根叫标准差。方差与标准差是描述数据分布特征的重要的统计量,它们是反映数值型数据离散程度最主要、最常用的方法。
根据总体数据和样本数据计算方差及标准差时,计算公式略有不同。

式中Xi是数值序列中的单个数值, 是这组数值的平均值,N是总体数值的个数,n是样本数值的个数。
计算样本方差与标准差时之所以与总体不同,是因为计算样本方差或标准差时,是要把它作为总体方差或标准差的估计量,统计上对估计量要求满足一些条件(一致性、无偏性、有效性),为满足无偏性条件,样本方差计算时,分母要用n-1,而不是n。
【例题10·单选题】(2009年)某产品在5个地区的销售量分别为1500、2000、1000、3000、5000。则该销售量的极差为( )。
A.1000 B.1500 C.2000 D.4000
[答疑编号716030501]
『正确答案』D
『答案解析』极差也称全距,是一组数据中最大值与最小值之差。本题中最大值为5000,最小值为1000,所以极差=5000-1000=4000。
3.相关分析
所谓相关分析,是研究现象之间是否存在某种依存关系,并对具体有依存关系的现象探讨其相关方向以及相关程度,是研究随机变量之间的相关关系的一种统计方法。
变量之间的相关关系主要有线性相关和非线性相关、正相关和负相关等几种形式。
对两个变量间线性相关程度的测量称为简单相关系数。样本相关系数定义公式为:

式中,r为样本相关系数,COVXY为协方差,Sx、Sy分别是变量x和y的标准差。(注意:公式中分子分母求和表达式中应该是i=1到n,而不是n=1到n)
相关系数r的取值范围在-1~+1之间。
·r=1或r=-1时,表明变量间的关系为完全正相关或完全负相关,这是两种极端的情况,实际上表明两个变量之间是线性关系;
·r=0时,表明变量间不存在线性相关关系,可能是无相关,也可能是非线性相关;
·0 ·-l |r|愈接近于l,变量间相关程度愈高,|r|愈接近于0,相关程度愈低。 在一般情况下,总体相关系数p是未知的,一般是用样本相关系数r作为总体相关系数P的估计值。但由于存在样本抽样的随机性,样本相关系数并不直接反映总体相关程度,因而,计算出来的样本相关系数在多大程度上值得信赖,需要进行检验。 |r|<自由度(df)为(n-2)的t统计量t(n-2)、显著性为a(10%;5%)的相关系数(查相关系数表),其相关性是显著的。所谓“显著水平”或r=0,指的是很少会发生的概率。 (教材这句话是错误的,正确的表达为: 在实际中,因为研究目的、变量类型的不同,采用的相关分析也不同。比较常用的相关分析有二元定距变量的相关分析、二元定序变量的相关分析、偏相关分析和距离分析等。 (二)推论统计分析 推论统计是在随机抽样的基础上,根据部分资料(数据)推断总体的方法,也即利用样本资料对抽出样本的总体做出推论的方法。 1.单个样本的参数估计 参数是指总体的某一特征值,如均值、方差等,往往是未知数;而根据样本数据计算出来的均值、样本标准差、样本比例一般称为样本“统计量”。参数估计是根据样本统计量对总体未知参数进行某种估计推断。 (1)点估计。当总体分布的形式已知,但其中的一个或多个参数未知时,如果从总体中抽取一个样本,用该样本对未知参数作一个数值点的估计,称为参数的点估计。 例如:假设对北京1800万人的工资水平进行调查,一般情况下,需要进行抽样调查,假设抽取1000个样本,得出的平均工资为2500元每月,这个2500就是样本的平均值,用 来表示,方差为200,所谓的点估计就是直接用样本的均值和方差来表示总体的均值和方差,即北京1800万人的平均工资就是2500元,方差为200。 点估计有多种方法,如矩法、最大似然法、最小二乘法等。 (2)区间估计。区间估计是用一个区间估计总体未知参数。设x1…,xn是来自总体的一个样本,对于给定的α(0<α<1),若有两个统计量θ1 (x1,…,x2)和θ2 (x1,…,xn),使得:P(θ1<θ>θ2)=1—α,则称1—α为信度(或置信度、置信概率),(θ1θ2)是θ的信度为1—α的置信区间,α称为显著性水平。 置信区间给出了区间估计的精确程度,区间越小精确度越高。置信概率给出了区间估计的可靠性。 例如1800万人的工资进行区间估计时,取α为10%,置信区间为(2300,2700),就表示北京1800万人的平均工资μ有90%的概率落在2300到2700元之间。或者说进行100次估计时,有大约90次是位于2300到2700之间,有大约10次位于2300到2700之外。 ①总体方差σ2已知时,总体均值μ的区间估计(采用Z统计量) 置信度为l一α时,总体均值μ的置信区间为: 即: ,那么 是区间信度下的临界点,称可靠性系数。信度越高,可靠性系数越大。 是区间估计时已知n和σ,对应一定的信度的置信区间的半径,也就是估计时的最大允许误差。 ②总体方差σ2未知时,总体均值μ的区间估计(采用t统计量) 如果总体服从正态分布,但σ2未知,可以用样本标准差S代替σ建立置信区间。此时统计量不是服从标准正态分布,而是服从自由度(df)为n-1的t分布。 此时,总体均值μ在置信度为1-α下的置信区间为: 2.单个样本的假设检验 参数估计和假设检验是统计推断的重要组成部分,它们都是利用样本信息对总体状况做出某种推断(判断),但是推断的角度不同。 ·参数估计是用样本统计量估计总体参数,估计前总体参数是未知的。(例如,对北京市1800万人平均工资进行调查,参数估计就是指在调查之前不知道平均工资是多少,然后采用抽样调查,抽取1000个样本进行调查,这1000人的平均工资是2500,就认为1800万人的平均工资是2500) ·假设检验则是先对总体参数的值提出一个假设,然后利用样本信息,根据抽样分布的原理去检验原先提出的假设是否成立。(例如,对北京市1800万人平均工资进行调查,假设检验就是指在调查之前假设这1800万人的平均工资是3000,然后采用抽样调查,抽取1000个样本进行调查,利用这1000人的平均工资数来判断3000的假设对不对) 进行假设检验时,通常经过以下步骤: (1)提出原假设和替换(备择)假设。预先所设的这一假设称为原假设,用H0表示。与原假设相对的假设是替换假设,它是原假设经检验不成立被拒绝接受时,所应接受的与原假设相对立的情况,用H1表示。 (2)确定并计算检验统计量。 总体方差σ2已知时,应用Z统计量(服从正态分布),计算公式为: 总体方差σ2未知时,应用t统计量(服从t分布),计算公式为: 式中: 为样本均值,μ0为原假设的参数值,σ(S)为总体(样本)标准差 (3)规定显著性水平α,并确定接受域与拒绝域的临界值。通常可取α=0.05或α=0.01,查出 或者 的值,即接受域与拒绝域的临界值。 (4)做出统计决策。 总体方差已知,用Z统计量检验: 如果|Z|< ,则检验统计量的值位于接受域,接受原假设,拒绝替换假设; 如果|Z|> ,则检验统计量的值位于拒绝域,拒绝原假设,接受替换假设。 总体方差未知,用t统计量检验: 如果|t|< ,则检验统计量的值位于接受域,接受原假设,拒绝替换假设; 如果|t|> ,则检验统计量的值位于拒绝域,拒绝原假设,接受替换假设。 二、多元统计分析 (一)多元回归分析 多元线性回归是简单线性回归的推广,指的是多个因变量对多个自变量的回归。其中最常用的是只限于一个因变量但有多个自变量的情况,也叫多重回归。 设随机变量Y与一般变量x1,x2…,xp,的线性回归模型为: y=β0+β1x1+β2x2+βpxp+ξ 其中,β0,β1,β2,…,βp是p+1个未知参数,β0称为回归常数,β1,β2,…,βp称为回归系数。y称为被解释变量,而x1,x2…,xp是P个可以精确测量并可控制的一般变量,称为解释变量,ξ称为随机干扰项。 当P=1时,即为一元线性回归模型。对一个实际问题,如果我们获得n组观测数据 (xi1,xi2,…xip;yi),i=1,2,…n,则线性回归模型可表示为: 例如,一个企业的销售量视为y,它可能受到多个变量的影响:价格、广告费支出等等,然后我们有2000到2009年所有这些变量的相关数据,就可以列出方程式,解出相关参数β。利用上述式子就可以对以后年度进行预测。 为了方便地进行模型的参数估计,对回归方程要做如下一些基本假定:(1)自变量与因变量之间存在线性关系;(2)随机误差项具有0均值和等方差;(3)E(ξ)=0;(4)无自相关;(5)残差与自变量之间相互独立;(6)无共线性。 在计算过程中应注意的问题是:(1)样本量不得少于30条记录;(2)自变量与因变量都应该是连续性数字型变量;(3)分类/等级变量可以采取哑变量(通常取值为0或1)。 计算出结果之后,要进行检验。常用的检验方法有R(复相关系数)检验、F检验、t检验、DW检验等。 (二) 列联表分析 列联表分析属于多元描述统计分析方法。在市场研究中有着广泛的应用。 列联表是观测数据按两个或更多属性(定性变量)分类时所列出的频数表。 一般来说,如果总体中的个体可按两个属性A与B分类,A有r个等级X1,X2,…… ,Xr,B有c个等级Y1,Y2,…… ,YC,从总体中抽取大小为n的样本,设其中有nij个个体的属性属于等级Xi和Yj,nij称为频数,将r×c个nij排列为一个r行c列的二维列联表,简称r×c表。若所考虑的属性多于两个,也可按类似的方式做出列联表,称为多维列联表。 由于属性或定性变量的取值是离散的,因此多维列联表分析属于离散多元分析的范畴。列联表只是检验变量之间是否相关,而非检验变量之间的因果关系。一般使用X2分布来进行独立性检验。 例如,我们针对消费者购买某种彩电时考虑的属性进行调查。题目这样设计: 当您购买彩电时,请在品牌、价格、款式和质量中挑出对您最重要的一个因素并在相应的表格中填写“1”,然后找出第二个重要的因素并在相应的格子中填写“2”,依次分别在第三和第四个格子里填写“3”和“4” 品牌 价格 款式 质量 彩电 单纯从上面的表格是看不出不同年龄段的人对彩电品牌重要性的认识是否有明显不同,这时就要用X2分布来进行独立性检验。 (三) 方差分析 方差分析,又称“变异数分析”或“F检验”,用于两个或两个以上样本均数差别的显著性检验。在市场调研中,方差分析适用于实验数据、调查数据和观察数据的分析。 在方差分析中,若涉及的因素只有一个,称为单因素方差分析,若涉及的因素为两个或两个以上,称为多因素方差分析。 例如,某连锁店要测量其自主品牌商品的价格弹性,随机从其连锁店中抽取24家店参与实验,分三个价位,每个价位抽取8家,并对各店一周的销售情况进行监测,以此看看在价格优惠条件下是否会对销售量产生显著效果。 例如,在列联表分析中所举的例子,我们已经知道不同年龄段对彩电品牌重要性的评价分布是不同的,但无法明确不同年龄段的消费者关于彩电品牌重要性评价的排序情况。这时就可以通过平均值比较和方差分析来实现。即先计算各年龄段对彩电品牌重要性评价的均值,然后进行不同年龄段均值的比较。 无论是单因素方差分析还是多因素方差分析,其步骤一般为: (1)明确因变量与自变量,建立原假设; (2)计算总方差、组间方差、组内方差,建立方差表; (3)显著性检验,即用F检验; (4)分析结果。 (四)聚类分析 聚类分析也称群分析或类分析,是对样品或变量进行分类的一种多元统计方法,目的在于将相似的事物归类。 对样品(指标的观测值)的分类被称为Q型聚类分析;对变量(指标)的分类被称为R型聚类分析。 变量如何选择,取决于聚类的目的。 具体来说,变量的类型有三种尺度: (1)间隔尺度,即变量用连续的量来表示,如果存在绝对零点,又称比例尺度;例如,长度、重量、时间等。在调研中不常见。 (2)有序尺度,即变量用有序的等级来表示,有次序关系,但没有数量表示;例如将十家啤酒公司的产量按高低自1排至10。 (3)名义尺度,即变量用一些“类”来表示,这些类之间没有等级和数量关系,相似物体的集合称为类。例如“1”代表男性,“2”代表女性。 不同类型的变量,在聚类分析中,处理方式各不一样。聚类分析方法主要有系统聚类法、样品聚类法、动态聚类法、模糊聚类法、图论聚类法和聚类预报法等。 【例题11·单选题】(2009年)在市场调研过程中,对样品的分类称为( )。 A.R型聚类分析 B.Q型聚类分析 C.X型聚类分析 D.T型聚类分析 [答疑编号716030601] 『正确答案』B 『答案解析』对样品的分类被称为Q型聚类分析。 (五)判别分析 判别分析是根据表明事物特点的变量值和它们所属的类求出判别函数,根据判别函数对未知所属类别的事物进行分类的一种分析方法。 与聚类分析不同,它需要已知一系列反映事物特性的数值变量及其变量值。 例如,企业可以根据往年的年度宏观经济指标、企业生产销售情况、销售费用的指标把以往各年的市场情况区分为畅销、平销和滞销三种,那么怎么样根据现有资料判断(预测)下一年产品是畅销、平销,还是滞销,这就属于判别分析。 根据判别的组数 两组判别分析 多组判别分析 根据判别函数的形式 线性判别 非线性判别 根据判别时处理变量的方法不同 逐步判别 序贯判别 根据判别标准的不同 距离判别 Fisher判别 Bayes判别 (六)因子分析 因子分析是研究如何以最少的信息丢失将众多原有变量浓缩成少数几个代表变量间关系的因子,并使因子具有一定的命名解释性。 其基本思想是,根据相关性大小把原始变量分组,使得同组内的变量之间相关性较高,不同组的变量间相关性较低,每组变量代表一个基本结构,并用一个不可观测的综合变量表示,这个基本结构称之为“公共因子”。 因子分析的基本步骤是.(1)确定研究变量;(2)计算所有变量的相关矩阵;(3)构造因子变量;(4)因子旋转,(5)计算因子得分。 例如:研究消费者的生活方式,通常采用心理描述测试法,即采用一系列关于对社会活动、价值观念等内容的陈述,请消费者根据自己的情况做出评价。调查中采用7分评价法, 1分表示“非常同意”,7分表示“非常不同意”。经事先的小样本测试筛选,最终的测试语句为:(20个) A.我喜欢购买新潮的东西 1 2 3 4 5 6 7 B.在其他人眼中我是很时髦的 C.我用穿着来表达个人性格 D.我对自己的成就有很大期望 E.生命的意义是接受挑战和冒险 F.我会参加/自学一些英语和电脑课程来接受未来的挑战 G.我习惯依计划行事 H.我喜欢品味独特的生活 I.放假时我喜欢放纵自己,什么事都不做 J.无所事事会使我感到不安 K.我的生活节奏很紧凑 L.优柔寡断不是我的处事方式 M.经济上的保障对我来说是最重要的 N.我选择安定和有保障的工作 O.我宁愿少休息多工作,以多挣些钱 P.我很容易与陌生人结交 Q.我活跃于社交活动 R.我对朋友有很大影响力 S.我很注意有规律的饮食习惯 T.我定期检查存款余额,以免入不敷出 由于测试的语句实际上是一系列相关因素的陈述,很多语句之间存在一定的相关性,通过因子分析则可以将系列相关因素综合为一个因子。 表1:因子分析的结果 组合因子 因子中包含的陈述(相关系数大于0.5) 因子含义 因子1 A、B、C、H 对时尚的观点 因子2 D、E、F、J、K 个人的事业性与进取性 因子3 M、N、O 对经济利益的看法 因子4 P、Q、R 社交能力与影响力 因子5 S、G、I、T 生活的计划性 因子分析在市场调研中有着广泛的应用,主要包括:消费者使用习惯和态度研究(U&A);品牌形象和特性研究|服务质量调查;个性测试;形象调查,市场划分识别;顾客、产品及行为分类。 (七)结合分析 结合分析,也称交互分析,在欧美国家的市场调研中被广泛应用。 结合分析的基本假设是,产品或研究对象是由一系列的属性所构成的,例如,电脑产品的属性为品牌、显示器、CPU、内存、硬盘等,而各属性又有一定的水平,如显示器有l4英寸、15英寸、l7英寸等,CPU可能有奔腾5、赛扬、K6等。 消费者的购买抉择过程是基于对这些属性的权衡与考虑做出的理性选择,因而,结合分析一般步骤为: (1)确定产品或服务的属性与属性水平; (2)将产品的所有属性与属性水平通盘考虑,并采用正交设计的方法将这些属性与属性水平进行组合,生成一系列虚拟产品; (3)请消费者对虚拟产品进行评价,通过打分、排序等方法调查消费者对虚拟产品的喜好、购买的可能性等; (4)计算属性的效用、计算属性的模型和方法主要包括最小二乘法回归、多元方差分析; (5)解释结果; (6)评估信度和效度,常用的有拟合优度和t检验等; (7)市场预测与市场模拟。 在市场调研中,结合分析可用于如下几个方面.(1)决定各种属性在消费者选择品牌(产品)时的相对重要性;(2)估计不同属性水平的市场占有率;(3)确定最受欢迎品牌的属性水平组合,(4)根据消费者对属性水平喜好的相似性,进行消费者市场分类;(5)应用于新产品概念识别;(6)竞争分析,(7)定价研究;(8)广告研究;(9)销售分布等。
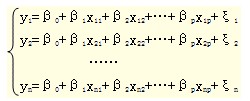






 中级经济基础
中级经济基础