第二十三章 时间序列
一、时间序列及其分类
统计对事物进行动态研究的基本方法是编制时间序列。
时间序列也称动态数列,是将某一统计指标在各个不同时间上的数值按时间先后顺序编制形成的序列。
时间序列由两个基本因素构成:(1)被研究现象所属时间,(2)反映该现象一定时间条件下数量特征的指标值。同一时间序列中,各指标值的时间单位一般要求相等。
时间序列按照其构成要素中统计指标值的表现形式,分为绝对数时间序列、相对数时间序列和平均数时间序列三种类型。
绝对数时间序列是由绝对数指标值按时间先后顺序排列后形成的序列。依据指标值的时间特点,绝对数时间序列又分为时期序列和时点序列。
由绝对数时间序列可以派生出相对数和平均数时间序列。它们是由同类相对数或平均数指标值按时间先后顺序排列后形成的序列。
表4—8 我国1991~1997年若干国民经济指标资料
|
|
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
|
国内生产总值 |
21 618 |
26 638 |
34 634 |
46 759 |
58 478 |
67 885 |
74 772 |
【例题1·单选题】统计对事物进行动态研究的基本方法是编制( )。
A.指数 B.回归方程 C.频数分布表 D.时间序列
[答案]D
【例题2·多选题】将某一统计指标在各个不同时间上的数值按时间先后顺序编制形成的序列称为( )。
A.时间序列 B.相关分析 C.动态数列
D.回归分析 E.指数分析
[答案]AC
【例题3·多选题】构成时间序列的基本因素是( )。
A.被研究现象的计量单位
B.被研究现象的分组情况
C.被研究现象的频数分布
D.反映该现象一定时间条件下数量特征的指标值
E.被研究现象所属时间
[答案]DE
【例题4·多选题】按照其构成要素中统计指标值的表现形式,时间序列分为( )。
A.绝对数时间序列 B.日时间序列
C.相对数时间序列 D.年时间序列
E.平均数时间序列
[答案]ACE
【例题5·多选题】(2008年)依据指标值的时间特点,绝对数时间序列分为( )。
A.时期序列 B.时点序列 C.相对数时间序列
D.平均数时间序列 E.整数时间序列
[答案]AB
【例题6·多选题】(2006年)下表中能源生产总量是( )时间序列。
我国l997~2003年能源生产总量
|
年份 |
1997 |
1998 |
1999 |
2000 |
200l |
2002 |
2003 |
|
能源生产总量 |
132 410 |
124 250 |
109 126 |
106 988 |
120 900 |
138 369 |
160 300 |
A.相对数 B.时期 C.绝对数 D.平均数 E.时点
[答案]BC
二、时间序列的水平分析
(一)发展水平
发展水平是时间序列中对应于具体时间的指标数值。在绝对数时间序列中,发展水平就是绝对数;在相对数和平均数时间序列中,发展水平表现为相对数或平均数。
时间序列中第一项的指标值称为最初水平,最末项的指标值称为最末水平,处于二者之间的各期指标值称为中间水平。
根据各期指标值在计算动态分析指标时的作用来划分,又可以分为基期水平和报告期水平。
【例题·单选题】时间序列中对应于具体时间的指标数值称为( )。
A.变量 B.发展水平 C.增长量 D.发展速度
[答案]B
(二)平均发展水平
平均发展水平也称序时平均数或动态平均数,是对时间序列中各时期发展水平计算的平均数,它可以概括性描述现象在一段时期内所达到的一般水平。时间序列类型不同,计算方法也不同。
1.绝对数时间序列序时平均数的计算
(1)由时期序列计算序时平均数
对于时期序列,序时平均数计算公式为:
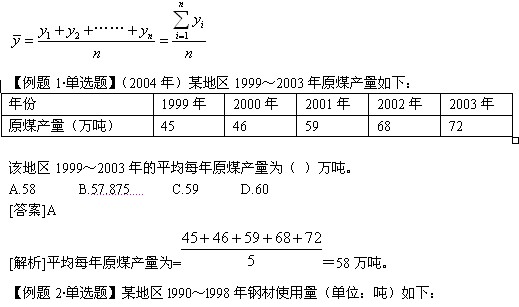
|
年份 |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
|
使用量 |
1316 |
1539 |
1561 |
1765 |
1726 |
1960 |
1902 |
2013 |
2446 |
该地区1990-1998年钢材年均使用量为( )。
A.1 726吨 B.1 750.6吨 C.1 803.1吨 D.1 846.7吨
[答案]C
[解析]年均使用量=(1316+1539+1561+1765+1726+1960+1902+2013+2446)/9=1803.1
(2)由时点序列计算序时平均数
第一种情况,由连续时点计算。又分为两种情形。
一种是资料逐日登记且逐日排列,可采用简单算术平均数方法计算,计算公式同上:
该企业3~6月份平均职工人数为( ) 。
A.1 500人 B.1 400人 C.1 445人 D.1 457人
[答案]D
|
|
计算方法 | |||
|
绝对数时间序列序时 平均数的计算 |
时期序列 |
—— |
| |
|
时点序列 |
连续时点 |
资料逐日登记且逐日排列,即已掌握了整段考察时期内连续性的时点数据 |
| |
|
资料登记单位仍是1天,但实际上只是在指标值发生变动时才记录一次 |
| |||
|
间断时点 |
间隔相等 |
| ||
|
间隔不等 |
| |||
|
相对数或平均数时间序列序时平均数 |
| |||
(三)增长量与平均增长量
1.增长量
增长量是报告期发展水平与基期发展水平之差,反映报告期比基期增加(减少)的绝对数量。用公式表示为:
增长量=报告期水平一基期水平
根据基期的不同确定方法,增长量可分为逐期增长量和累计增长量。
(1)逐期增长量
逐期增长量是报告期水平与前一期水平之差。它表明现象逐期增加(减少)的绝对数量。
(2)累计增长量
累计增长量是报告期水平与某一固定时期水平(通常是时间序列最初水平)之差,它表明报告期比该固定时期增加(减少)的绝对数量。
同一时间序列中,累计增长量等于相应时期逐期增长量之和。
【例题1·单选题】增长量是( )。
A.报告期发展水平与基期发展水平之差
B.报告期发展水平与基期发展水平之和
C.报告期发展水平与基期发展水平之比
D.最末水平与最初水平之比
[答案]A
【例题2·单选题】逐期增长量是( )。
A.报告期水平与前一期水平之差
B.报告期水平与某一固定时期水平(通常是时间序列最初水平)之差
C.时间序列中逐期增长量的序时平均数
D.报告期发展水平与基期发展水平之比
[答案]A
2.平均增长量
平均增长量是时间序列中逐期增长量的序时平均数,它表明现象在一定时段内平均每期增加(减少)的数量。其计算公式为:
(i=1,2……n)
根据逐期增长量与累计增长量之间的数量关系,平均增长量还可以用下式表现:
【例题1·多选题】(2006年)根据基期的不同,增长量可分为( )。
A.累计增长量 B.平均增长量 C.逐期增长量
D.环比增长量 E.最终增长量
[答案]AC
【例题2·单选题】(2007年)平均增长量是时间序列中( )的序时平均数。
A.累计增长量
B.报告期水平与某一固定时期水平(通常是时间序列最初水平)之差
C.逐期增长量
D.报告期发展水平
[答案]C
[答案]A
[解析]平均增长量=累计增长量/(时间序列项数-1)=(55-35)/(5-1)=5。
三、时间序列的速度分析
(一)发展速度与增长速度
1.发展速度
发展速度是以相对数形式表示的两个不同时期发展水平的比值。计算公式为:
发展速度=报告期水平/基期水平
由于基期选择的不同,发展速度有定基与环比之分。
(1)定基发展速度是报告期水平与某一固定时期水平(通常是最初水平)的比值,用ai表示
【例题1·单选题】(2004年、2006年)环比发展速度等于( )。
A.逐期增长量与其前一期水平之比
B.累计增长量与最初水平之比
C.报告期水平与最初水平之比
D.报告期水平与其前一期水平之比
[答案]D
【例题2·单选题】(2005年、2006年、2007年)以2000年为基期,我国2002、2003年广义货币供应量的定基发展速度分别是137.4%和164.3%,则2003年与2002年相比的环比速度发展是( )。
A.16.4% B.19.6% C.26.9% D.119.6%
[答案]D
[解析]相应时期的环比发展速度等于两个相邻时期定基发展速度的比。环比速度发展=164.3%/137.4%=119.6%
【例题3·单选题】已知某地区以1990年为基期,1991年~l996年财政收入的环比发展速度分别为l15.71%、118.23%、l08.01%、l31.9%、l22.95%、l01.54%,1990年为基期的l996年财政收入的定基发展速度为( )。
A.40.55% B.243.30% C.101.54% D.43.30%
[答案]B
[解析]定基发展速度=l15.71%×118.23%×l08.01%×l31.9%×l22.95%×l01.54%=243.30%
2.增长速度
增长速度是报告期增长量与基期水平的比值。计算公式为:
增长速度=报告期增长量/基期水平
由于基期选择的不同,增长速度也有定基与环比之分。
(1)定基增长速度
用 表示,定基增长速度=报告期累计增长量/基期水平=定基发展速度-1
(2)环比增长速度
用Bi表示,环比增长速度=报告期逐期增长量/基期水平=环比发展速度-1
发展速度与增长速度应用中要注意的问题是:定基增长速度与环比增长速度不能像定基发展速度与环比发展速度那样互相推算。定基增长速度与环比增长速度之间的推算,必须通过定基发展速度和环比发展速度才能进行。
【例题·单选题】(2007年)已知某地区2002-2006年社会消费品零售总额的环比增长速度分别为4%、6%、9%、10%,则这一时期该地区社会消费品零售总额的定基增长速度为( )。
A.4%×6%×9%×l0%
B.(4%×6%×9%×l0%)+1
C.(104%×106%×109%×l10%)-1
D.104%×l06%× 109%×l10%
[答案]C
(二)平均发展速度与平均增长速度
平均发展速度反映现象在一定时期内逐期发展变化的一般程度,平均增长速度则反映现象在一定时期内逐期增长(降低)变化的一般程度。
平均增长速度与平均发展速度之间的数量关系:平均增长速度=平均发展速度-1。
目前计算平均发展速度通常采用几何平均法。几何平均法也称水平法。平均发展速度的计算公式:
对数进行分析。
2.速度指标的数值与基数的大小有密切关系。在环比增长速度时间序列中,各期的基数不同,因此,运用这一指标反映现象增长的快慢时,往往要结合水平指标的分析才能得出正确结论。“增长1%的绝对值”,是进行这一分析的指标。它反映同样的增长速度,在不同时间条件下所包含的绝对水平。计算公式为:
增长1%的绝对值=逐期增长量/环比增长速度
【例题1·单选题】(2005年、2004年)在环比增长速度时间序列中,由于各期的基数不同,运用速度指标反映现象增长的快慢时往往需要结合( )这一指标分析才能得出正确结论。
A.报告期水平 B.增长1%的绝对值
C.累计增长量 D.平均增长量
[答案]B
【例题2·单选题】(2005年)“增长1%的绝对值”反映的是同样的增长速度在不同( )条件下所包含的绝对水平。
A.计量单位 B.数据类型 C.时间 D.调查方法
[答案]C
【例题3·多选题】时间序列的速度分析指标有( )。
A.发展速度 B.平均发展速度 C.增长速度
D.平均增长速度 E.平均增长量
[答案]ABCD
















 中级经济基础
中级经济基础