根据高等教育出版社消息,2022年全国硕士研究生招生考试大纲在9月14日正式发布!考试大纲规定了各学科的考试范围和考试要求,具体考到什么程度,考研大纲中都有明确说明。考试大纲和历年考研试题才是考研复习过程中重点参考权威官方资料。
《2022全国硕士研究生招生考试管理类专业学位联考综合能力考试大纲》已经公布。就近几年来看,管理类联考考试内容已经趋于稳定,考纲变化不大。中公教研团队就2022年的大纲,为各位考生做大纲解析。对于各位参加2022考研的考生,希望你在接下来的三个多月的时间里,能够合理计划,查漏补缺,克服短板,巩固基础,理清框架,磨炼技巧,每天都过得充实,体会到满满的成就感。对于各位计划参加 2023 或者以后年份考试的考生,希望你通过此解析对管理类联考有基本了解。
2022秋季考前冲刺已经开始,希望通过金秋三个月的努力,同学们对于管理类联考初等数学的学习能够达到各类题型熟练掌握的程度,但是想要真正做好对于2022考研的把控,最终在十二月份的初试中独占鳌头,首先要做的就是熟悉我们22的考试大纲,熟悉考试大纲我们才能做到有的放矢,方能知己知彼,百战不殆。接下来就由中公教研团队为大家分析一下,代数与函数的相关考纲要求。
代数部分贯穿初、高中知识内容,知识点较难、灵活度高,在历年试题中穿插考查,综合性较强。代数主要包含六部分知识内容:整式,分式及其运算、函数、代数方程,不等式,数列、等差数列、等比数列。
一、考纲内容
从考纲发布的内容来看,“代数”板块主要包括以下内容:
1. 整式
(1)整式及其运算
(2)整式的因式与因式分解
2. 分式及其运算
3. 函数
(1)集合
(2)一元二次函数及其图像
(3)指数函数、对数函数
4. 代数方程
(1)一元一次方程
(2)一元二次方程
(3)二元一次方程组
5. 不等式
(1)不等式的性质
(2)均值不等式
(3)不等式求解
一元一次不等式(组),一元二次不等式,简单绝对值不等式,简单分式不等式。
6. 数列、等差数列、等比数列
通过对比历年初数的考试大纲不难看出,今年初数的考纲基本保持稳定,没有发生变化。换言之,今年的初数试卷中,代数章节仍然会占据一个相对较大的比重,无论从分值还是题量抑或是难度上,都会和过去的试题一样,成为同学们考研路上的一只“拦路虎”。针对于此,同学们在复习过程中,一定要多花时间,把握侧重点,根据考纲要求, 做好复习工作。
二、考纲解读
今年,考纲中再次明确了代数部分又包含了以下内容:整式、分式及其运算、函数、代数方程、不等式、数列。以此足见考试内容多且广,那么在这些所有考察的科目中,我们的整式,函数以及不等式依旧是我们复习过程中的重中之重,既是常考点也是难点,可以说,只要攻克了以上三个难点,那么同学们在22年的考试中,初数的理想成绩不是梦。
关于整式,必须给各位考生强调的就是这当中的整式除法。整式及其运算今年再度被列为考试大纲的要求,那么在过往的考试当中,大部分的整式除法都离不开多项式除法,多项式除法是各位考生在接下来9-12月阶段训练的一个重点,训练中不能仅仅拘泥于准确度,对于速度同样要做提升,要做到快且准!特别地,在针对多项式除法中有一个非常常用的“超级武器”——因式/余式定理,各位考生务必注意理解,做到融会贯通。余式定理的本质是化除为乘且令除式为0,解出的根代入被除式中与因式/余式之间建立等量关系,从而解出因式/余式。这是试题中一贯的考查形式,希望各位考生掌握。
关于函数可能是整个代数甚至整个初数的最重要也是最核心的知识点了,因为涉及到的函数种类多,而二次函数、指对数函数的难度相对比较大,所以复习的时候一定要把握重点和难点,务必攻克函数这一道难关。22年的考纲中仍然明确规定了对于函数的要求。在此为各位考生提出关于函数复习的几点要求:
(1)务必会画所有考纲中要求的函数图像,考纲要求掌握的函数包括:正比例函数、一次函数、二次函数、指数函数、对数函数,只要熟练掌握函数图像,函数的各大性质皆可通过函数图像读出;
(2)务必了解函数的单调性和奇偶性,同样也是包含上述的所有函数,皆要做到熟练掌握。特别地,二次函数的奇偶性和指对数函数的单调性尤为常考,所以各位考生务必引起重视。
不等式部分在考试中也是较为普遍的存在,许多题目都离不开不等式的运用,单独命题的点在于:不等式的基本运算性质、一元二次不等式、均值不等式。其中一元二次不等式和均值不等式较为灵活,为常见考点,一元二次不等式多会和其他问题进行结合,复习中重在理解一元二次不等式、一元二次方程、一元二次函数的关系。在此务必给考生强调三个点:
(1)绝对值不等式,这里尤其需要注意的是三角不等式。三角不等式不常考,一旦考到,必是一道有区分度的题,所以考生务必做好此方面的针对性训练;
(2)高次不等式,无理不等式等非常规不等式,做好归纳总结工作;
(3)均值不等式,这是一个必考点,几乎年年都要涉及到,而关联的知识点也比较丰富,可以借助应用题,数列等等作为载体,进而间接考查均值不等式,所以考生在这方面灵活运用的能力需要提升。
除了这三个重点以外的知识点,我们也要对其考试的定位进行了解,分式及其运算内容较少,需要格外注意分母不为零的问题,除此之外,分式的出现会包含分子和分母,那整式的内容也可以在其中进行考察;数列部分比较固定,基本上就围绕等差数列、等比数列两部分的基本公式进行命题,稳定在每年两道题左右。
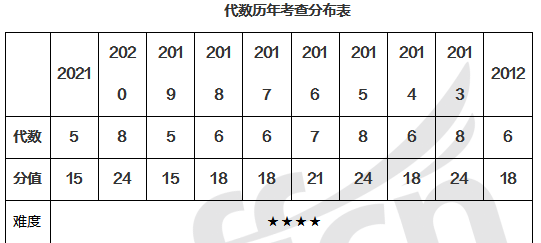
三、试题展示
观察历年试题分值分布,我们可以看出代数部分和几何部分在我们考试中占分比是最大的部分,代数部分难度较大,几何部分难度适中,让我们来做道题目感受一下吧!

这道题重点考察如何利用一元二次函数图像来解决一元二次函数中比较复杂的问题,学生在利用图像分析这方面能力普遍需要加强。






